首页 MachineLearn

混淆矩阵 ( Confusion Matrix ) 是分类模型的一种评估指标。它是使用一种特定的矩阵来呈现算法性能的可视化效果，通常是监督学习。(非监督学习，通常用匹配矩阵：m atching matrix ) 其每一列代表预测值，每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆（也就是一个 class 被预测成另一个 class ）。

# 举例

我们以 是否感染新冠肺炎的模型来演示 混淆矩阵。

按照定义，我们可以得到如下矩阵。

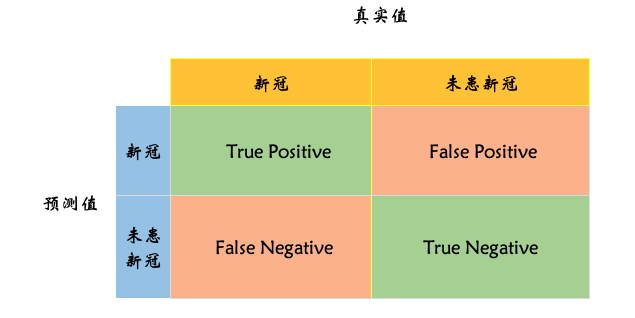
横向看上图，预测感染新冠为 Positive , 即为阳性， 未感染新冠为 Negative , 即 阴性。

纵向看上图，预测正确的为 True , 预测错误的为 False .

所以会得出 如下四种结果；

  • True Positive : TP , 真阳性，即预测结果是新冠，真实值也是新冠。
  • True Negative : TN , 真阴性，即预测结果是未感染，真实也未感染新冠。

这两个结果是模型预测正确的结果，也是我们最想得到的部分，这两部分所占比重越大，模型效果越好。对应上图中绿色部分。其占比成为模型的准确率。

  • False Positive : FP , 假阳性，即预测得了新冠，但是实际人并没有感染新冠。这种的属于误报。其占比属于误报率。在统计学中， FP 又称为 第一类错误 ( Type Error I ，被判定为真的假)
  • False Negative : FN , 假阴性，即预测没有感染新冠，但是实例已经感染了新冠。这种属于漏报率。其占比成为漏报率。 FN 又称为 第二类错误 ( Type Error II , 被判定为假的真)

这两种情况，是模型预测错误的场景，所占比重越低越好。对应上图中红色部分。

# 指标

很多指标都是从混淆矩阵发展出来的。在例子中，我们已经知道了准确率，误报率，漏报率。

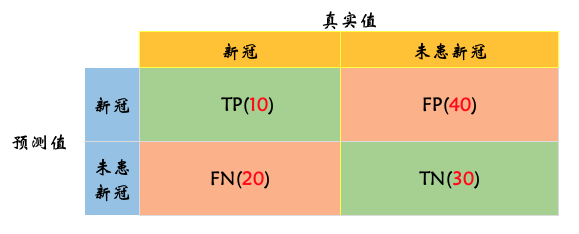
以图为例，我们来详细的看下分类模型中混淆矩阵的相关指标.

# 🔥🔥准确率

accuracy=TP+TNTP+TN+FP+FNaccuracy=\frac{TP+TN}{TP+TN+FP+FN}

那么，本例子中的准确率，就是： (10+30)/100=40%

理解成本最低，但不要滥用。在样本不均衡情况下，指标结果容易出现较大偏差；

# 🔥🔥精确率

精确率是判断模型识别出来的结果有多精确的指标。对应到信用评分的产品上，就是模型找到的真的坏人（对应混淆矩阵中的）的比率占模型找到的所有坏人（对应混淆矩阵中的 ）的比率。

precision=TPTP+FPprecision=\frac{TP}{TP+FP}

用于关注筛选结果是不是正确的场景，宁可没有预测出来，也不能预测错了。比如，在刷脸支付的场景下，我们宁可告诉用户检测不通过，也不能让另外一个人的人脸通过检测。

精确率，又称为 查准率.

# 漏报率 (FNR)

FNR=FNFN+TPFNR = \frac{FN}{FN + TP}

那么，本例子中的漏报率，就是： 20/(10+20)=66.67%

# 误报率

FPR=FPFP+TPFPR = \frac{FP}{FP + TP}

那么，本例子中的漏报率，就是： 40/(40+30)=37.14%

# 🔥🔥召回率

表示实际患者中，预测患病成功的概率. Recall Rate 又称为 Sensitive , 查全率。预测感染占实际感染的额比率。即预测为真占实际为真的比率。

Sensitive(TPR)=TPTP+FNSensitive(TPR)=\frac{TP}{TP+FN}

用于关注筛选结果是不是全面的场景，“宁可错杀一千，绝不放过一个”。

# Specificity

表示未患病中，预测未患病成功的概率。

Specificity(TNR)=TNTN+FPSpecificity(TNR)=\frac{TN}{TN+FP}

这两个指标的出现，能更好的帮你比较模型间的差异，并在其中做出取舍。例如当两个模型的 Accuracy 相近时，如果你更看重于预测患病的效果，你应该选 Sensitivity 值较高的；相反，如果你更看重于预测未患病的效果，你就应该选择 Specificity 较高的。

# 🔥🔥F1 Score

F1 可以综合反应精确率 和召回率。 F1 值越高，代表模型在精确率 和 召回率的综合表现越好。

F1=2×preciosion×recallprecision+recallF1=\frac{2 \times preciosion \times recall}{precision+recall}

# P-R 曲线

P 表示查准率 (或者精确率), 计算公式是: \frac{TP}

R 表示查全率 (或者召回率，Sensitive), 计算公式是: \frac{TP}

P-R 曲线是描述查准率 / 查全率变化的曲线， P-R 曲线定义如下：根据学习器的预测结果（一般为一个实值或概率）对测试样本进行排序，将最可能是 “正例” 的样本排在前面，最不可能是 “正例” 的排在后面，按此顺序逐个把样本作为 “正例” 进行预测，每次计算出当前的 P 值和 R 值，如下图所示：

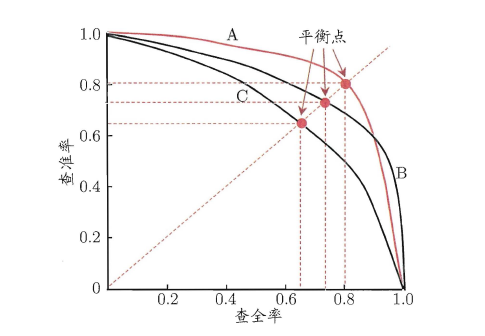
# 如何看 P-R 曲线？

P-R 曲线如何评估呢？若一个 学习器A 的 P-R 曲线被另一个 学习器B 的 P-R 曲线完全包住，则称： B 的性能优于 A 。若 A 和 B 的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。但一般来说，曲线下的面积是很难进行估算的，所以衍生出了 “平衡点”（ Break-Event Point ，简称 BEP ），即当 P=R 时的取值，平衡点的取值越高，性能更优。

P 和 R 指标有时会出现矛盾的情况，这样就需要综合考虑他们，最常见的方法就是 F-Measure，又称 F-Score。F-Measure 是 P 和 R 的加权调和平均，即：

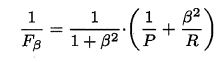
特别地，当 β=1 时，也就是常见的 F1 度量，是 P 和 R 的调和平均，当 F1 较高时，模型的性能越好。

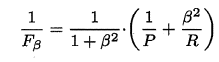
有时候我们会有多个二分类混淆矩阵，例如：多次训练或者在多个数据集上训练，那么估算全局性能的方法有两种，分为宏观和微观。简单理解，宏观就是先算出每个混淆矩阵的 P 值和 R 值，然后取得平均 P 值 macro-P 和平均 R 值 macro-R ，在算出 Fβ 或 F1 ，而微观则是计算出混淆矩阵的平均 TP 、 FP 、 TN 、 FN ，接着进行计算 P 、 R ，进而求出 Fβ 或 F1 。

# 🔥🔥ROC 曲线 和 AUC

ROC 曲线与 P-R 曲线十分类似，都是按照排序的顺序逐一按照正例预测，不同的是 ROC 曲线以 “真正例率”（ True Positive Rate ，简称 TPR , 计算公式: TPTP+FN\frac{TP}{TP+FN}）为横轴，纵轴为 “假正例率”（ False Positive Rate ，简称 FPR , 计算公式: FPTN+FP\frac{FP}{TN+FP}, 又称为特异性。 Specificity 。）， ROC 偏重研究基于测试样本评估值的排序好坏。

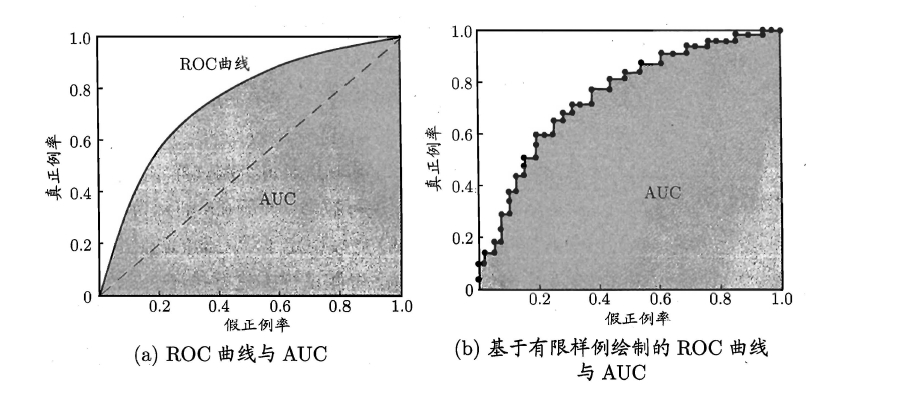
简单分析图像，可以得知：当 FN=0 时， TN 也必须 0 ，反之也成立，我们可以画一个队列，试着使用不同的截断点（即阈值）去分割队列，来分析曲线的形状， (0,0) 表示将所有的样本预测为负例， (1,1) 则表示将所有的样本预测为正例， (0,1) 表示正例全部出现在负例之前的理想情况， (1,0) 则表示负例全部出现在正例之前的最差情况。

# 怎么看 ROC 曲线呢？

若一个学习器 A 的 ROC 曲线被另一个学习器 B 的 ROC 曲线完全包住，则称 B 的性能优于 A 。若 A 和 B 的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。 ROC 曲线下的面积定义为 AUC （ Area Uder ROC Curve ），不同于 P-R 的是，这里的 AUC 是可估算的，即 AOC 曲线下每一个小矩形的面积之和。易知： AUC 越大，证明排序的质量越好， AUC 为 1 时，证明所有正例排在了负例的前面， AUC 为 0 时，所有的负例排在了正例的前面。

AUC 计算公式:

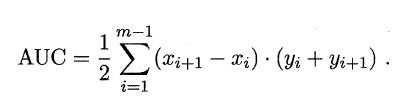
# 代价敏感错误率与代价曲线

上面的方法中，将学习器的犯错同等对待，但在现实生活中，将正例预测成假例与将假例预测成正例的代价常常是不一样的，例如：将无疾病–> 有疾病只是增多了检查，但有疾病–> 无疾病却是增加了生命危险。以二分类为例，由此引入了 “代价矩阵”（ cost matrix ）。

在非均等错误代价下，我们希望的是最小化 “总体代价”，这样 “代价敏感” 的错误率为:

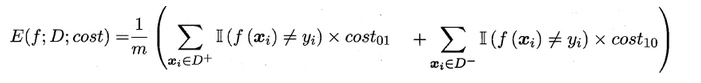
同样对于 ROC 曲线，在非均等错误代价下，演变成了 “代价曲线”，代价曲线横轴是取值在 [0,1] 之间的正例概率代价，式中 p 表示正例的概率，纵轴是取值为 [0,1] 的归一化代价。


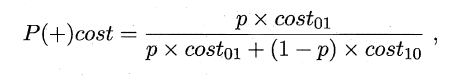
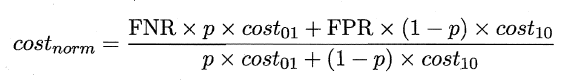
代价曲线的绘制很简单：设 ROC 曲线上一点的坐标为 ( TPR ， FPR ) ，则可相应计算出 FNR ，然后在代价平面上绘制一条从 ( 0 ， FPR ) 到 ( 1 ， FNR ) 的线段，线段下的面积即表示了该条件下的期望总体代价；如此将 ROC 曲线图的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价，如图所示：

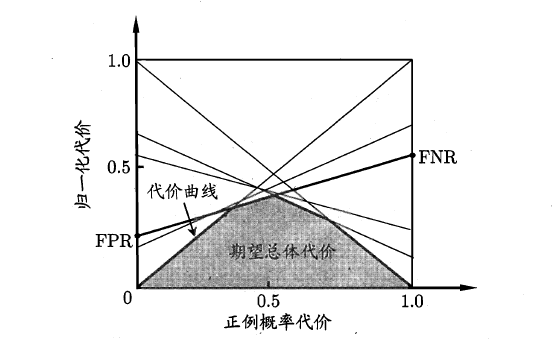
以上就是 由混淆矩阵引申出来的指标了，当然这些指标都是用来评估分类模型的。下篇文章，我们再来介绍回归模型的评估指标。

# 指标图

# 最后

希望和你一起遇见更好的自己

qrcode