首页 MachineLearn

k-近邻算法 ，英文名: K Nearest Neighbor 算法 又叫 KNN算法 ，这个算法是机器学习里面一个比较经典的算法， 总体来说 1 算法是相对比较容易理解的算法.

# 定义

如果一个样本在特征空间中的 k 个最相似 (即特征空间中最邻近) 的样本中的大多数属于某一个类别，则该样本也属于这个类别。

KNN 算法最早是由 Cover 和 Hart 提出的一种分类算法。应用场景有字符识别、文本分类、图像识别等领域。

# 算法的理解

举一个例子来，来分析一下 KNN 算法的实现原理

假设我们现在有几部电影，如下图:

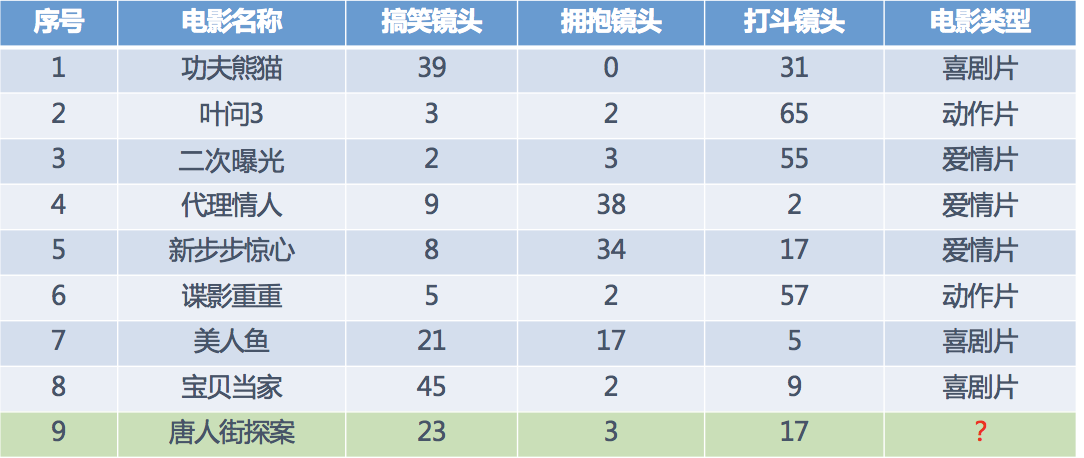
我们要 根据 搞笑镜头，拥抱镜头，打斗镜头的个数 这三个特征来预测出 《唐人街探案》所属的电影类型.

我们使用 KNN算法 思想来实现预测。

将样本中特征作为坐标抽，建立坐标系。从而建立特征空间。本例中，分别把 搞笑镜头，拥抱镜头，打斗镜头 作为 x,y,z 轴。然后把计算出每个样本和 《唐人街探案》 的距离，选择距离最近的前 k 个 ( KNN中的k ) 样本，这 k 个样本大多数所属的电影类别就是 《唐人街探案》的电影类型。

特征空间：是指已特征为坐标轴简历的一种特征的坐标系，可能是多维的。

那你可能对 距离 是如何计算的，有点疑惑。计算距离的方式有很多种。
先学习一下最简单的 欧氏距离。(初中都学过的！)

在二维坐标系中， 我们可以使用一下方式来计算出两个点的距离。

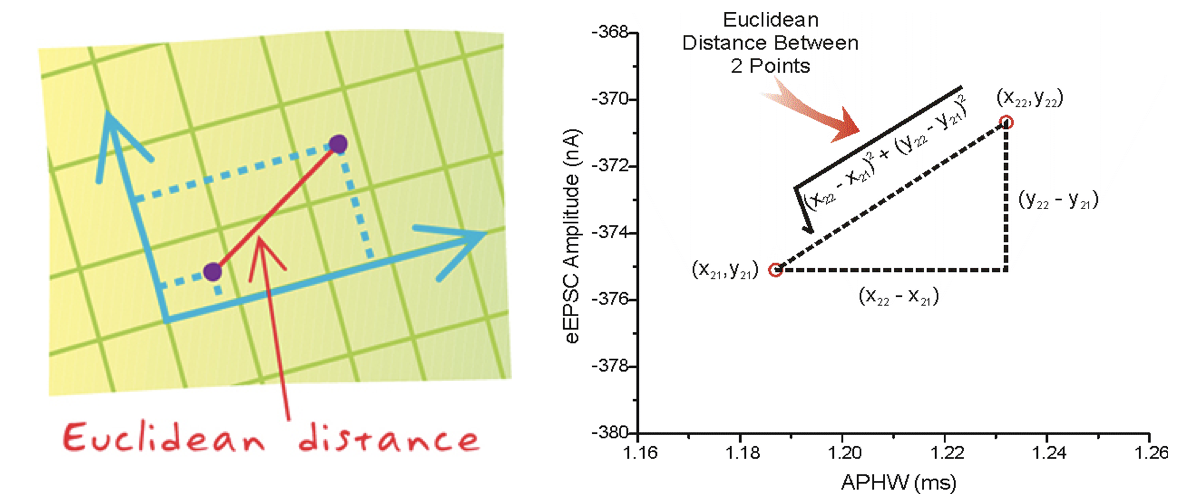
在多维的特征空间中，我们也可以使用同样的方式来计算欧式距离。如下图：

那计算一下样本集中的欧式距离，如下图:

并计算出了最近的 5 个样本中有三个喜剧片类型，2 两个爱情片类型。 那根据 KNN 就是喜剧片类型。

这就是 KNN算法 的核心思想了。

这个例子中，我们选则了 最近的 5 个样本，也就是 k=5 的时候，会有三个喜剧片类型，两个爱情片类型。这个 5 是如何选择的呢？

# k 值的选择

K值 选择问题，李航博士的一书「统计学习方法」上所说：

  1. 选择较小的 K 值，就相当于用较小的领域中的训练实例进行预测，“学习” 近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是 “学习” 的估计误差会增大，换句话说， K值 的减小就意味着整体模型变得复杂，容易发生过拟合；

  2. 选择较大的 K值 ，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且 K 值的增大就意味着整体的模型变得简单。

  3. K=N （ N 为训练样本个数），则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。

在实际应用中， K值 一般取一个比较小的数值，例如采用交叉验证法 ( cross validation )（简单来说，就是把训练数据在分成两组：训练集和验证集）来选择最优的 K 值。对这个简单的分类器进行泛化，用核方法把这个线性模型扩展到非线性的情况，具体方法是把低维数据集映射到高维特征空间。

# KNN 的优化

KNN 算法需要计算所有的样本数据和预测数据的距离，需要选择出距离预测数据最近的 k 个样本数据的预测归类。在庞大的数据量面前，计算所有样本数据距离，显然是不可取的。为了避免每次都重新计算一遍距离， KNN 算法提供了多种优化方法， 比如 KD-tree , ball_tree , brute . 这几种优化方式的具体实现逻辑，我会在后面的几篇文章中挨个分析。

# 距离的计算

KNN 算法，最重要的就是距离。 除了上文提到的欧式距离，还有其他计算距离的方法吗？

有。

除了欧式距离，还有 曼哈顿距离，

# 曼哈顿距离

在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是 “曼哈顿距离”。曼哈顿距离也称为 “城市街区距离”( City Block distance )。如下图:

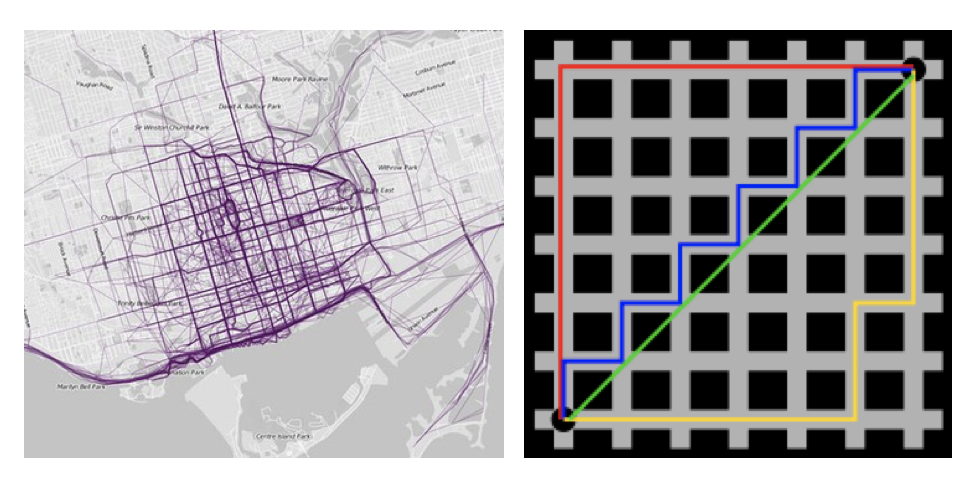
计算公式见下图:

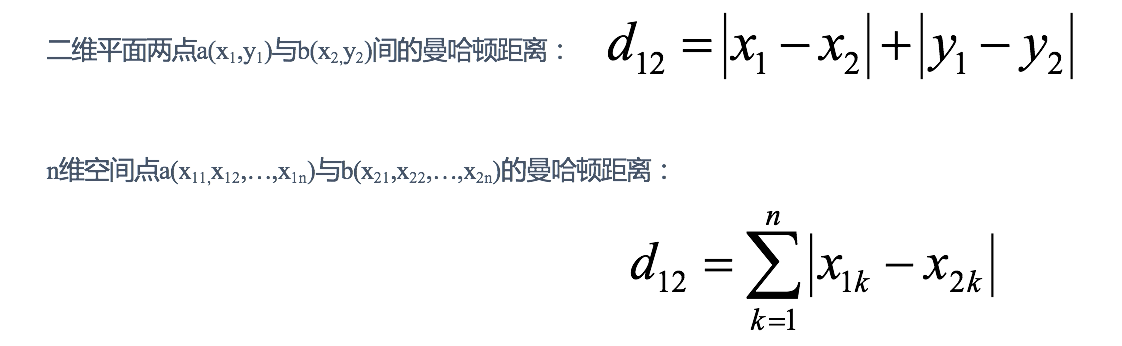
# 切比雪夫距离 (Chebyshev Distance)

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻 8 个方格中的任意一个。国王从格子 (x1,y1) 走到格子 (x2,y2) 最少需要多少步？这个距离就叫切比雪夫距离。

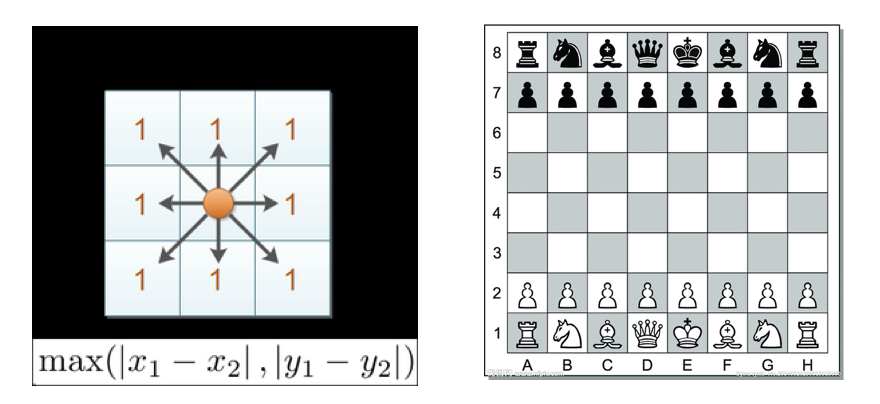
计算公式见下图:

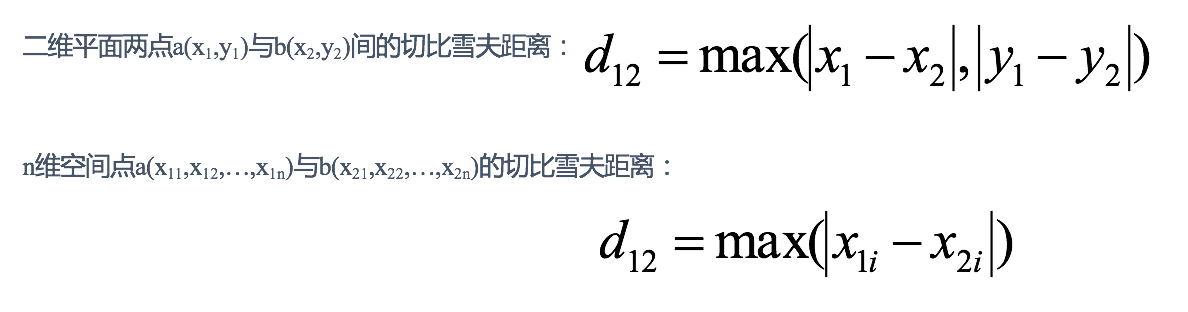
# 闵可夫斯基距离 (Minkowski Distance)

闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

两个 n 维变量 a(x11,x12,…,x1n) 与 b(x21,x22,…,x2n) 间的闵可夫斯基距离定义为：

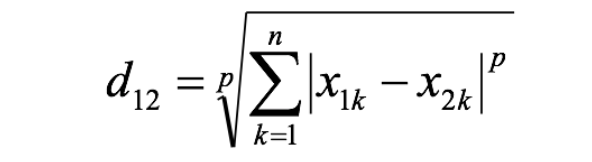
其中 p 是一个变参数：
当 p=1 时，就是曼哈顿距离；
当 p=2 时，就是欧氏距离；
当 p→∞ 时，就是切比雪夫距离。

根据 p 的不同，闵氏距离可以表示某一类 / 种的距离。

小结：
1 闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:
e.g. 二维样本 (身高 [单位:cm] , 体重 [单位:kg] ), 现有三个样本： a(180,50) ， b(190,50) ， c(180,60) 。
a 与 b 的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于 a 与 c 的闵氏距离。但实际上身高的 10cm 并不能和体重的 10kg 划等号。

2 闵氏距离的缺点：
​ (1) 将各个分量的量纲 ( scale )，也就是 “单位” 相同的看待了；
​ (2) 未考虑各个分量的分布（期望，方差等）可能是不同的。

# 标准化欧氏距离 (Standardized EuclideanDistance)

标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。

思路：既然数据各维分量的分布不一样，那先将各个分量都 “标准化” 到均值、方差相等。假设样本集 X 的均值 ( mean ) 为 m ，标准差 ( standard deviation ) 为 s ， X 的 “标准化变量” 表示为：

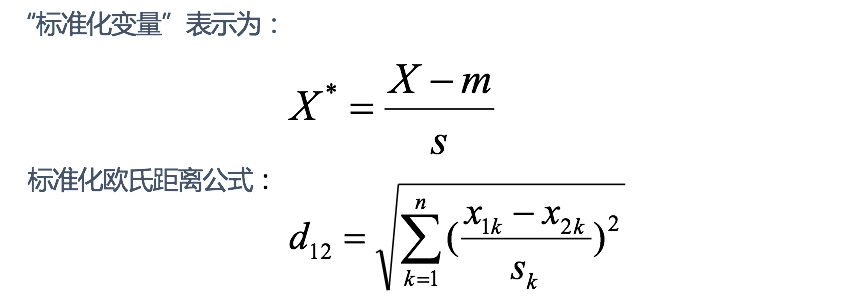
如果将方差的倒数看成一个权重，也可称之为加权欧氏距离 ( Weighted Euclidean distance )。

# 余弦距离 (Cosine Distance)

几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。

二维空间中向量 A(x1,y1) 与向量 B(x2,y2) 的夹角余弦公式：

两个 n 维样本点 a(x11,x12,…,x1n) 和 b(x21,x22,…,x2n) 的夹角余弦为：

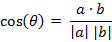
即:

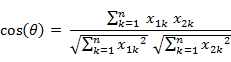
夹角余弦取值范围为 [-1,1] 。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值 1 ，当两个向量的方向完全相反余弦取最小值 -1

# 汉明距离 (Hamming Distance)

两个等长字符串 s1 与 s2 的汉明距离为：将其中一个变为另外一个所需要作的最小字符替换次数。

例如：

1
2
3
The Hamming distance between "1011101" and "1001001" is 2. 
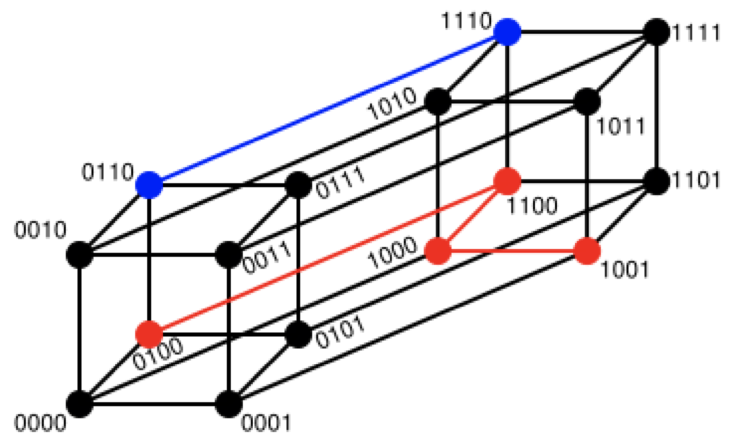
The Hamming distance between "2143896" and "2233796" is 3. 
The Hamming distance between "toned" and "roses" is 3.

汉明重量：是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4 。因此，如果向量空间中的元素 a 和 b 之间的汉明距离等于它们汉明重量的差 a-b 。

应用：汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中，为了增强容错性，应使得编码间的最小汉明距离尽可能大。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。

# 杰卡德距离 (Jaccard Distance)

杰卡德相似系数 ( Jaccard similarity coefficient )：两个集合 A 和 B 的交集元素在 A ， B 的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号 J(A,B ) 表示：

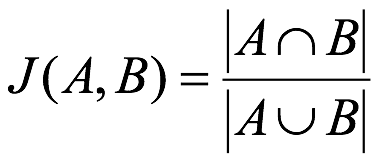
杰卡德距离 ( Jaccard Distance )：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：

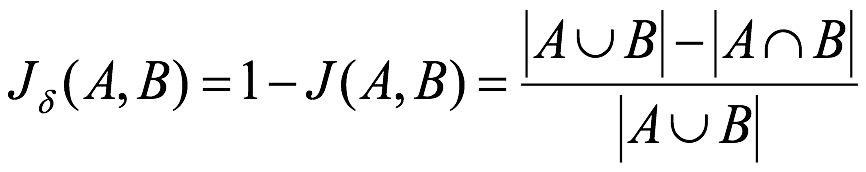
# 马氏距离 (Mahalanobis Distance)

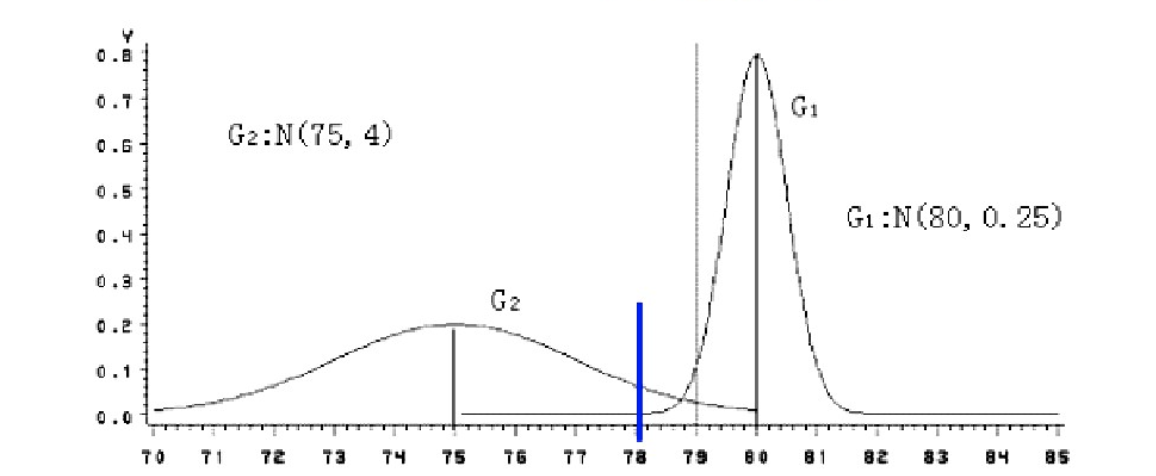
下图有两个正态分布图，它们的均值分别为 a 和 b ，但方差不一样，则图中的 A 点离哪个总体更近？或者说 A 有更大的概率属于谁？显然， A 离左边的更近， A 属于左边总体的概率更大，尽管 A 与 a 的欧式距离远一些。这就是马氏距离的直观解释。

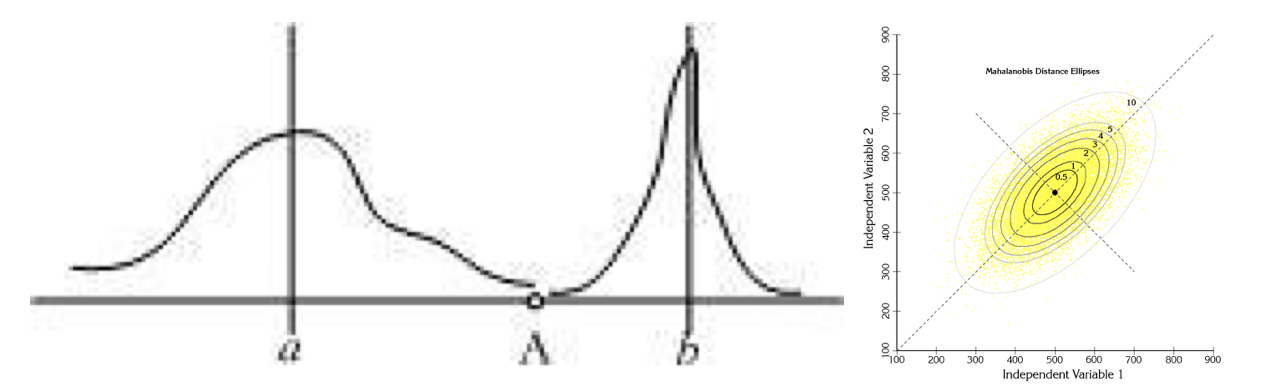
马氏距离是基于样本分布的一种距离。

马氏距离是由印度统计学家马哈拉诺比斯提出的，表示数据的协方差距离。它是一种有效的计算两个位置样本集的相似度的方法。

与欧式距离不同的是，它考虑到各种特性之间的联系，即独立于测量尺度。

马氏距离定义：设总体 G 为 m 维总体（考察 m 个指标），均值向量为 μ=（μ1，μ2，… ...，μm，） , 协方差阵为 ∑=（σij） ,

则样本 X=（X1，X2，… …，Xm，） 与总体 G 的马氏距离定义为：

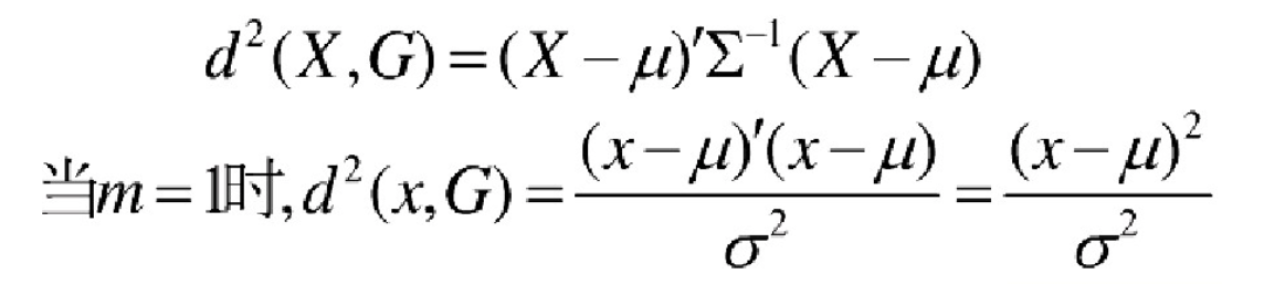
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为 ∑ 的随机变量的差异程度：如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离；如果协方差矩阵为对角矩阵，则其也可称为正规化的欧式距离。

# 马氏距离特性：

1. 量纲无关，排除变量之间的相关性的干扰；

2. 马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

3 . 计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

4. 还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如三个样本点 (3,4) ， (5,6) ， (7,8) ，这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

# 欧式距离 & 马氏距离：

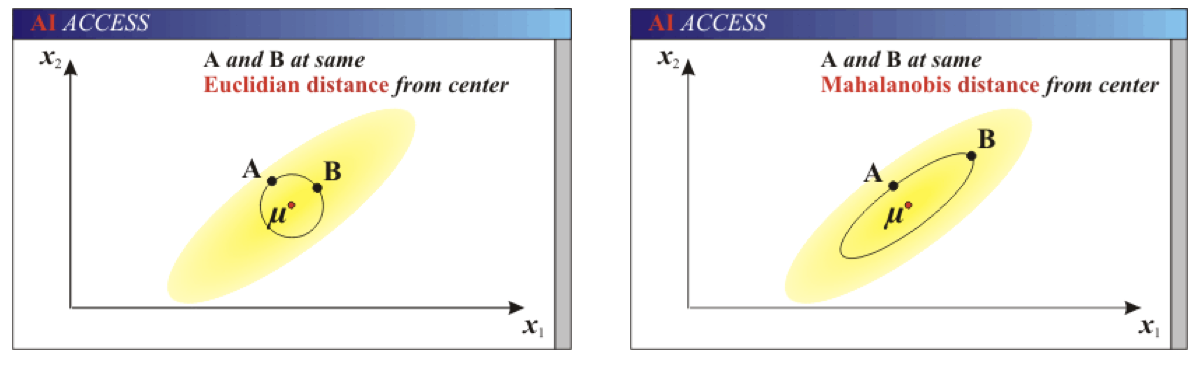
举例：

已知有两个类 G1 和 G2 ，比如 G1 是设备 A 生产的产品， G2 是设备 B 生产的同类产品。设备 A 的产品质量高（如考察指标为耐磨度 X ），其平均耐磨度 μ1=80 ，反映设备精度的方差 σ2(1)=0.25 ; 设备 B 的产品质量稍差，其平均耐磨损度 μ2=75 ，反映设备精度的方差 σ2(2)=4 .

今有一产品 G0 ，测的耐磨损度 X0=78 ，试判断该产品是哪一台设备生产的？

直观地看， X0 与 μ1 （ 设备A ）的绝对距离近些，按距离最近的原则，是否应把该产品判断 设备A 生产的？

考虑一种相对于分散性的距离，记 X0 与 G1 ， G2 的相对距离为 d1 ， d2 , 则：

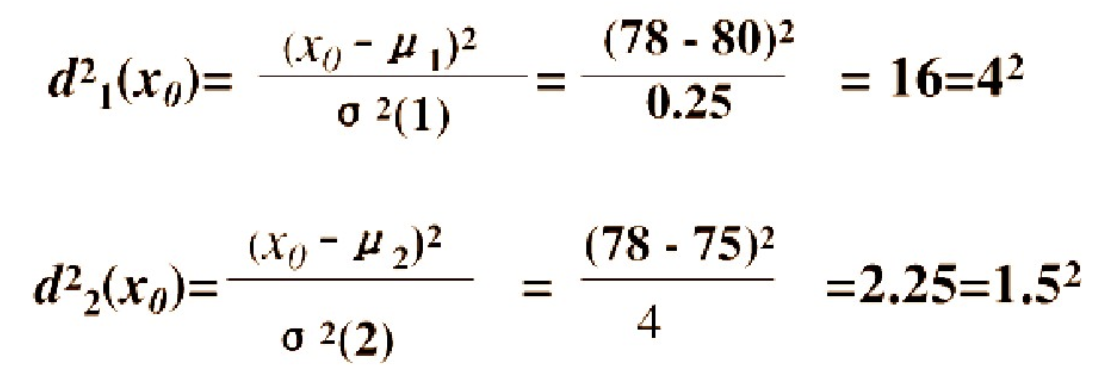
因为 d2=1.5 < d1=4 ，按这种距离准则，应判断 X0 为设备 B 生产的。

设备 B 生产的产品质量较分散，出现 X0 为 78 的可能性较大；而 设备A 生产的产品质量较集中，出现 X0 为 78 的可能性较小。

这种相对于分散性的距离判断就是马氏距离。

# 案例

# 预测鸢尾花种类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier


def iris_demo():
    # 1.准备数据
    iris = load_iris()

    # 2.数据基本处理
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)

    # 3.特征工程
    # 3.1 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4.机器训练(模型训练)
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1  方法1：比对真实值和预测值
    predict_data = estimator.predict(x_test)
    print("预测值为: \n", predict_data)
    print("比对真实值和预测值;\n", predict_data == y_test)

    # 5.2  方法2: 直接计算正确率
    score = estimator.score(x_test, y_test)
    print("正确率:", score)

# 输出结果

1
2
3
4
5
6
7
预测值为: 
 [0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2]
比对真实值和预测值;
 [ True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True  True  True  True False  True  True  True  True  True
  True  True  True  True  True  True]
正确率: 0.9666666666666667

# 使用 GSCV 优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier


def iris_demo():
    # 1.准备数据
    iris = load_iris()

    # 2.数据基本处理
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3.特征工程
    # 3.1 标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4.机器训练(模型训练)
    estimator = KNeighborsClassifier()

    # 4.1 准备要调的超参数
    param_dict = {"n_neighbors": [1, 3, 5]}
    # 4.2 创建 GridSearchCV,使用网格搜索和交叉验证
    estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)

    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1  方法1：比对真实值和预测值
    predict_data = estimator.predict(x_test)
    print("预测值为: \n", predict_data)
    print("比对真实值和预测值;\n", predict_data == y_test)

    # 5.2  方法2: 直接计算正确率
    score = estimator.score(x_test, y_test)
    print("正确率:", score)

    # 6. 直接查看评估结果哦
    print("在交叉验证中验证的最好结果：", estimator.best_score_)
    print("最好的参数模型：", estimator.best_estimator_)
    print("每次交叉验证后的准确率结果：\n", estimator.cv_results_)


if __name__ == '__main__':
    iris_demo()

# 输出结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
预测值为: 
 [0 2 1 2 1 1 1 1 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
 0]
比对真实值和预测值;
 [ True  True  True  True  True  True  True False  True  True  True  True
  True  True  True  True  True  True False  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True  True  True
  True  True]
正确率: 0.9473684210526315
在交叉验证中验证的最好结果： 0.9732100521574205
最好的参数模型： KNeighborsClassifier()
每次交叉验证后的准确率结果：
 {'mean_fit_time': array([0.0008928 , 0.00045244, 0.00044529]), 'std_fit_time': array([5.74547103e-04, 5.05512361e-06, 2.92218150e-06]), 'mean_score_time': array([0.00226967, 0.00184425, 0.00182239]), 'std_score_time': array([6.28895378e-04, 2.09757168e-05, 1.41269575e-05]), 'param_n_neighbors': masked_array(data=[1, 3, 5],
             mask=[False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}], 'split0_test_score': array([0.97368421, 0.97368421, 0.97368421]), 'split1_test_score': array([0.97297297, 0.97297297, 0.97297297]), 'split2_test_score': array([0.94594595, 0.89189189, 0.97297297]), 'mean_test_score': array([0.96420104, 0.94618303, 0.97321005]), 'std_test_score': array([0.01291157, 0.03839073, 0.00033528]), 'rank_test_score': array([2, 3, 1], dtype=int32)}

# 预测 facebook 签到位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV


def facebook_demo():
    # 准备数据
    data = pd.read_csv('./train.csv')
    print(data.head())

    # 2.数据基本处理

    ## 2.1 处理时间特征
    time = pd.to_datetime(data['time'], unit='s')
    time = pd.DatetimeIndex(time)

    data['hour'] = time.hour
    data['day'] = time.day
    data['weekday'] = time.weekday

    print(data.head(10))

    # 2.2.去掉签到少的地方
    place_count = data.groupby("place_id").count()
    place_count = place_count[place_count["row_id"] > 3]
    data = data[data["place_id"].isin(place_count.index)]

    # 2.3 确定特征和目标值
    x = data[['x', 'y', "accuracy", "day", "hour", "weekday"]]
    y = data[['place_id']]

    # 2.4 拆分数据集
    x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)

    # 3. 特征处理
    # 3.1 标准化处理
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4.机器学习
    # 4.1 实例化估计器
    estimator = KNeighborsClassifier()
    param_dict = {'neighbors': [1, 3, 5]}
    estimator = GridSearchCV(estimator=estimator, param_grid=param_dict)
    # 4.2 模型训练
    estimator.fit(x_train, y_train)

    # 模型评估
    print("\n最后预测的准确率为: ", estimator.score(x_test, y_test))

    print("\n在交叉验证中验证的最好结果:\n", estimator.best_score_)
    print("\n最好的参数模型:\n", estimator.best_estimator_)
    print("\n每次交叉验证后的验证集准确率结果和训练集准确率结果:\n", estimator.cv_results_)


if __name__ == '__main__':
    facebook_demo()

本案例来自 Kaggle 的题目，感兴趣的朋友可以登录:https://www.kaggle.com/navoshta/grid-knn/script 查看

# 最后

希望和你一起遇见更好的自己

qrcode