快速排序 - 数据结构与算法 | 方家小白 = 和你一起遇见更好的自己

# 快速排序思想

快速排序的核心思想也是分治思想。

快速排序主要要以待排数组中的某个数字为基准。将整个数组中的数据分为小于基准的一组和大于等于基于的一组.(或者是小于等于基准的一组和大于基于的一组), 分别对每组进行拆分，直到每组中只有一个数据。

递推公式如下:

假设 low 为待排数组中的起始索引. high 为待排数组中的终止索引. std 为基准的索引.

$quickSort(low,high) = quickSort(low,std-1)+quickSort(std+1,high)$

终止条件为:

$low>=high$

# 排序过程图

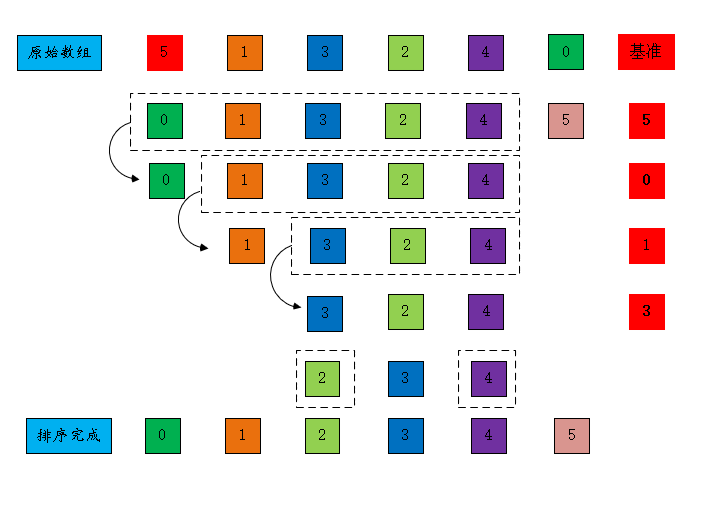
算法01-排序04-快速排序01.png

简单解释下:

我们首先选定基准，假设以本次递归的第一个数为基准，进行排序.
如图：第一次递归的基准为 5, 我把大于 5 的数，放在右侧，小于 5 的数放在左侧，(例子中没有大约 5 的数)，第二次以 0 为基准，把大于 0 的数，放在右侧，小于 0 的数，放在左侧。重复这样的逻辑，直到最后一次递归。

# 排序代码实现


void quick_sort(int *a, int low, int high) {

    if (low >= high) {
        return;
    }

    int i = low;
    int j = high;
    int std = a[low];
    while (i < j) {
        while (i<j&&a[j] >= std) {
            j--;
        }
        if (a[j] < std) {
            a[i++] = a[j];
        }
        while (i<j&&a[i] <= std) {
            i++;
        }
        if (a[i] > std) {
            a[j--] = a[i];
        }
    }
    a[i] = std;
    quick_sort(a, low, i - 1);
    quick_sort(a, i + 1, high);
}

# 快速排序的优化

之前说，快速排序的时间复杂度退化到 $O(n^2)$ 的主要原因是：分区点选的不够合理.

最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多.

为了提高排序算法的性能，我们也要尽可能的让每次分区都比较均匀.

比较常用，比较简单的选择分区点的方法有:

三数取中法

我们从某个区间的首，尾，中间，分别取出一个数，然后对比大小，取这三个数据的中间值作为分区点。也可以多取几个区间，取出中间值，然后在这些中间值，取出中间值。比如三数取中，五数取中，十数取中等等。

随机法

每次都从排序的区间中随机选择一个元素作为分区点。

这种方式，并不能保证每次分区点都选的比较好，但是从概率的角度来看，也不大可能出现每次分区点都选的很差的情况。所以时间复杂度退化为 $O(n^2)$ 的情况，可能性也不大。

# 快排算法评估

时间复杂度为最好情况下为 $O(nlogn)$ , 最坏情况下为 $O(n^2)$ , 平均情况下的时间复杂度为:
空间复杂度为 $O(n)$ , 是一种原地排序算法
是一种不稳定的排序算法.

注意：快排算法虽然在最坏情况下的时间复杂度为 $O(n^2)$ , 但是在平均情况下，时间复杂度为 $O(nlogn)$ ，不尽如此，快排的时间复杂度退化到 $O(n^2)$ 的概率非常小，我们也可以通过合理选择基准的方式来避免这总情况.

# 最后

期望与你一起遇见更好的自己

算法数据结构与算法排序快速排序分支思想排序