归并排序 - 数据结构与算法 | 方家小白 = 和你一起遇见更好的自己

将数组从中间分成前后两部分，然后对前后两部分分别进行排序，再将排好序的两部分合并在一起，这样整个数组就是有序的了。

归并体现的思想就是 分治思想 分而治之，将一个大问题分解成小的问题来解决。小问题解决了，大问题也就解决了.

这种分治的算法，一般都是递归的方式来求解。我们也尝试着写一个递归方式的归并排序。

写递归的程序，最重要的就是写 递推表达式和查找临界条件

根据归并排序的思想我们可写出这样的递推公式:

假设: low 为待排序数组的最小的索引. high 为待排序数组的最大索引. mid 为 (high+low)/2
那么: merge_sort(low,high) = merge(merge_sort(low,mid),merge_sort(mid+1,high))

对某个数组从下标 low 到 high 的排序，转换成了子问题从 low 到 mid 的排序和从 mid+1 到 high 的排序。当这两个子问题排好序之后，再将两个有序的子数组合并在一起，这样下标从 low 到 high 之间的数据也就都是排好序的了。

还有一个问题：终止条件是什么？终止条件就是子问题中的 low >= high , 这个时候，我们就可以终止递归了。

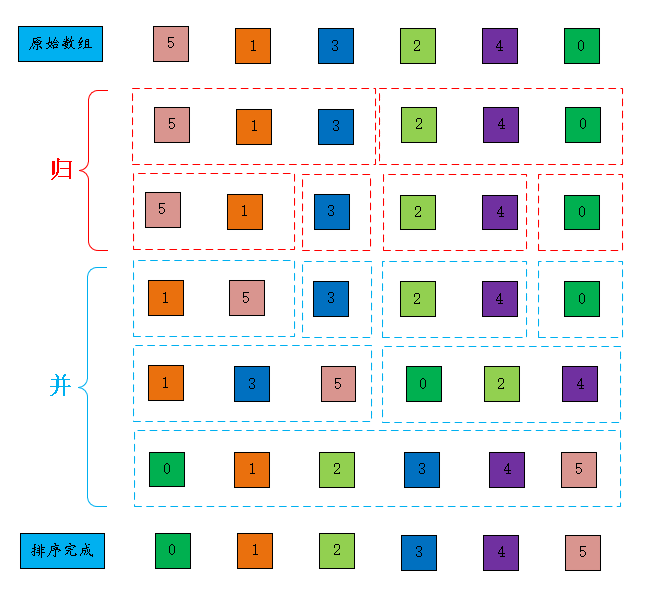
# 归并排序逻辑图

来一张归并排序过程的示意图吧

算法01-排序03-归并排序01

# 归并排序算法实现

void merge(int *a, int low, int high, int mid) {
    int temp_arr_length = high - low + 1;

    int t[temp_arr_length];

    int j = mid + 1;
    int i = low;
    int m = 0;
    // 判断大小
    for (; i <= mid && j <= high;) {
        t[m++] = a[i] < a[j] ? a[i++] : a[j++];
    }

    // 判断分组数量不相等时的情况
    while (j <= high) {
        t[m++] = a[j++];
    }
    // 判断分组数量不相等时的情况   
    while (i <= mid) {
        t[m++] = a[i++];
    }
    // 将中间表的数据赋值给原始的数组
    for (int i = 0; i < m; i++) {
        a[low + i] = t[i];
    }
}

void merge_sort(int *a, int low, int high) {

    if (low >= high) {
        return;
    }

    int mid = (low + high) >> 1;
    // 归
    merge_sort(a, low, mid);
    merge_sort(a, mid + 1, high);
    // 并
    merge(a, low, high, mid);
}

# 归并排序性能评估

归并排序是一个稳定的排序算法
归并排序的时间复杂度为 $O(nlogn)$
归并排序的空间复杂度为 $O(n)$

# 归并排序时间复杂度的推算

归并排序这种实现方式的时间复杂度的推算，也就是对递归的时间复杂度的推算。

不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成递推公式

递归的主要特征就是:
一个问题 a, 可以拆分为多个子问题 b,c, 那么求解 a 问题就转换成了求解子问题 b,c。b 和 c 解决之后，我们就把 b,c 的结果合并成 a 的结果.

那我们假设求解 a 问题的时间是 T (a), 求解问题 b,c 的时间为 T (b),T©, 那么我就可以得到这样的递推公式:

$T(a) = T(b) + T(c) + K$

其中， K 是解决完子问题 b , c 之后，合并为 a 问题所需要的时间。对于归并排序来讲， K 就是 merge 所需要的时间了.

# 那我们来详细的分析下归并排序时间复杂度:

假设:
对 n 个元素，进行归并排序的时间为 $T(n)$
那么:
分解成两个子数组排序的时间都是 $T(n/2)$
merge 函数合并两个有序子数组的时间复杂度是 $O(n)$

套用前面的公式:

当 n=1 时: $T(n) = C$ , 常量级的执行时间.
当 n>1 时: $T(n)=2*T(n/2)+n$

$\begin{aligned} T(n) &= 2*T(n/2)+n\\ &= 2 * (2 * T(n/4) + n/2) + n = 4 * T(n/4) + 2 * n \\ &= 4 * (2 * T(n/8) + n/4) + n = 8 * T(n/8) + 3 * n \\ &= 8 * (2 * T(n/16) + n/8) + n = 16 * T(n/16) = 4 * n \\ &= ....\\ &= 2^k * T(\frac{n}{2^k}) + k * n; \end{aligned}$

其中 $k$ 就是分裂的次数。拆分子问题的次数.

当 n=1, 则 k=0. , 即 $T(1) = T(\frac{n}{2^k})$ , ==> $\frac{n}{2^k}=1$ , 那么 $k=log_2n$

将 $k$ 代入公式

$\begin{aligned} & 2^k * T(\frac{n}{2^k}) + k * n \\ &= 2^{log_2n} * T(\frac{n}{2^{log_2n}}) + log_2n * n \\ &= C·n + n·log_2n \end{aligned}$

使用大 $O$ 表示法: $O(nlogn)$ .

归并排序的执行效率和要排序的原始数据的有序程度无关，所以不管最好情况和最坏情况下都是， $O(nlogn)$ .

# 最后

期望与你一起遇见更好的自己

算法数据结构与算法排序冒泡排序分治思想排序