首页 数据结构与算法

数据结构与算法 这一个模块 有两个最难的知识点，一个就是 递归，另一个就是 动态规划

我们今天来学习下递归这种实现方式。

个人认为，递归不是一种算法，就是一种语法。所以我就称它为一类问题的解决方法.

# 何为递归？

递归，去的过程叫递，回来的过程叫归。凡是递归类的问题，都能总结出一个递归公式.
比如: f(n+1)=f(n)+1f(n+1) = f(n) + 1, 我们用代码实现就是:

1
2
3
int f(n){
    return n==1?1:f(n-1)+1;
}

# 判断是否可用递归

要想使用递归来解决问题，要满足三个条件:

  • 一个问题的解可以分解为几个问题的解。
  • 这个问题和分解之后的问题，除了树据规模不一样，求解思路一模一样.
  • 存在递归终止条件。比如上例子中的f(n)=1f(n)=1

# 如何编写递归

# 找出递推公式！

递归写法的话，最重要的就是写出递推公式，其次就是，找到终止条件.

举个例子:

人民币的组合方式.

假设我有人民币 100 元，50 元，20 元，10 元，5 元，1 元的币种若干张，我想用这些花掉 70 元，我可以怎么花？

这个问题就可以转换成了，70 元有多少中组合方式 (A) -> 69 元有多少中组合方式 (B) + 65 元有几种组合方式 © + 60 元有几种组合方式 (D) + 50 元有几种组合方式 (E) + 20 元有几种组合方式 (F)。

也就是说，我们把一个问题 A 分解成了若干子问题 B,C,D,E,F. 我们解决了子问题 B,C,D,E,F。 那么对应的 A 问题，也就解决了。而且，在这问题里，我们只要关心 A 与其子问题的关系即可，不用关系其他的子问题与子问题的关系。屏蔽掉递归细节。

# 递归实现方案的注意点

  • 如果递归深度比较大的话，就会出现堆栈溢出的异常。
  • 递归的时候，要避免重复计算.
    这个的话，举个例子，就会很清晰了。斐波那契数列的计算.

斐波那契数列就是 当前项等于前两项之和.

以 fib (6) 为例，即求第 6 个数的数值。

如下图:

算法01-动态规划01-fib.png

我们会发现: fib (4),fib (3),fib (2) 都是重复计算的。

具体的解决方式呢，在 算法【动态规划】文章里，也有说过。

加入一个数据，来记录就行了.
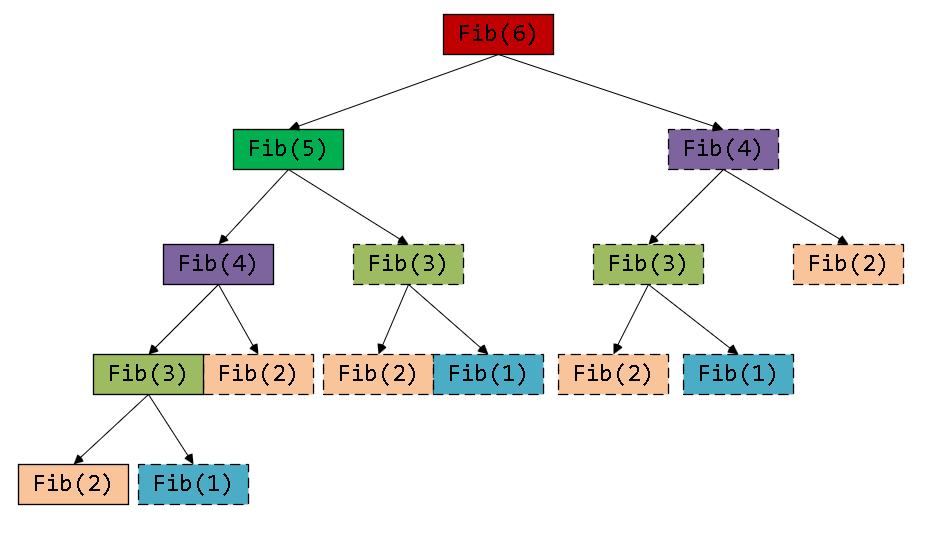算法01-动态规划01-fib02.png 其中虚线边框的就不用再计算了。

  • 一定要明确终止条件。不然就是死循环！

好了，以上就是递归的介绍。

# 最后

期望与你一起遇见更好的自己

期望与你一起遇见更好的自己