👉 动态规划其实就是动态递推 👈
# 要点
递归 + 记忆化 -> 递推 (自下而上的递推)
状态的定义,opt [n],dp [n],fib [n]
状态转移方程 (dp 方程), opt [n]=best_of (opt [n-1],opt [n-2])
最优子结构
# 例子# 斐波那契数列我们先使用递归的方式,我们实现斐波那契数列.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <stdio.h> int fib1 () int fib2 () int main () printf ("fib1(6)=%d\n" , fib1(6 )); printf ("fib2(6)=%d\n" , fib2(6 )); return 0 ; } int fib1 (int n) if (n <= 0 ) { return 1 ; } else if (n == 1 ) { return 1 ; } else { return fib1(n - 1 ) + fib1(n - 2 ); } } int fib2 (int n) if (n <= 1 ) { return 1 ; } else { return fib1(n - 1 ) + fib1(n - 2 ); } }
如下图:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 int fib3 (int n) int main () printf ("fib3(6)=%d\n" , fib3(6 )); return 0 ; } int mem[100 ];int fib3 (int n) if (n <= 0 ) { return 1 ; } else if (n == 1 ) { return 1 ; } else if (!mem[n]) { mem[n] = fib1(n - 1 ) + fib1(n - 2 ); } return mem[n]; }
这样我们就省去了个别节点的计算过程了。如下图
这样的话,我们把时间复杂度优化到了 O (n).
然后我们就可以发现:
1 fib(n) = fib(n-1) + fib(n-2);
这个就是我们的状态转移方程 (dp 方程)。
# 计算路线# 例题描述
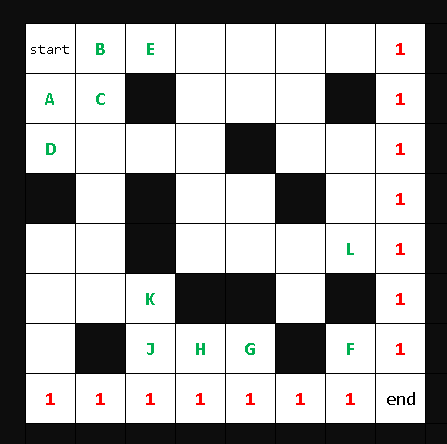
只能横着走或者竖着走,假设有一个人总 start 处,走到 end 处,一共有多少条路线?
# 分析
从 start 到 end 的所有路线,等于 B 到 end 路线加上 A 到 end 的路线。因为 start 要到 end,要么到 A, 从 A 走到 end, 要么到 B,从 B 走到 end。那么同理 B 到 end 就等于 C 到 end 的路线到 E 到 end 的路线。D 到 end 等于 C 到 end 的路线加上 D 到 end 的路线.
p a t h ( s t a r t , e n d ) = p a t h ( A , e n d ) + p a t h ( B , e n d ) path(start,end)=path(A,end) + path(B,end)
p a t h ( s t a r t , e n d ) = p a t h ( A , e n d ) + p a t h ( B , e n d )
同理:
p a t h ( A , e n d ) = p a t h ( D , e n d ) + p a t h ( C , e n d ) p a t h ( B , e n d ) = p a t h ( E , e n d ) + p a t h ( C , e n d ) path(A,end)=path(D,end) + path(C,end) \\ path(B,end) = path(E,end) + path(C,end)
p a t h ( A , e n d ) = p a t h ( D , e n d ) + p a t h ( C , e n d ) p a t h ( B , e n d ) = p a t h ( E , e n d ) + p a t h ( C , e n d )
一直到最下面的一行,最下面的这一行的每个点到 end 的路线只有一条,所以每个都是 1, 同样的最右侧的一列,每个都是 1. 如下图.
根据以上的推论我们尝试写出这样的代码:
1 2 3 4 5 6 7 8 9 int countPaths (int [][] grid,int row,int col) if (!validSquare(grid,row,col)){ return 0 ; } if (isEnd(grid,row,col)){ return 1 ; } return countPaths(grid,row+1 ,col) + countPaths(grid,row,col+1 ); }
我根据推论可以得出状态转移方程:
1 2 3 4 if a[i,j] == '白色' : opt[i,j] = opt[i+1 ,j] + opt[i,j+1 ] else : opt[i,j] = 0
# 程序实现1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int uniquePaths (int m, int n) int paths[m+1 ][n+1 ]; for (int i=m;i>0 ;i--){ paths[i][n] = 1 ; } for (int j =n; j>0 ;j--){ paths[m][j] = 1 ; } for (int i = m-1 ; i > 0 ; i--) { for (int j = n - 1 ; j > 0 ; j--) { paths[i][j] = paths[i+1 ][j] + paths[i][j+1 ]; } } return paths[1 ][1 ]; }
# DP vs 回溯 vs 贪心
回溯 (递归) - 重复计算
贪心 - 永远局部最优
DP - 记录局部最优子结构 / 多种记录值。(集两者之大成)
三者并没有明显的界限。贪心不是局部最优的时候,回溯避免了重复计算之后,就是了动态规划了。
# 例题# 爬楼梯# 题目描述假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
# 解析如下面的图:
因为我们只有两种走法,要么跨一个台阶,要么跨两个台阶。那么如图中我们爬到第 10 层台阶的走法就等于第 9 (10-1) 层台阶的走法和第 8 (10-2) 层台阶的走法的和。即 s t a i r s ( 10 ) = s t a i r s ( 9 ) + s t a i r s ( 8 ) stairs(10)=stairs(9)+stairs(8) s t a i r s ( 1 0 ) = s t a i r s ( 9 ) + s t a i r s ( 8 )
s t a i r s ( n ) = s t a i r s ( n − 1 ) + s t a i r s ( n − 2 ) stairs(n) = stairs(n-1) + stairs(n-2)
s t a i r s ( n ) = s t a i r s ( n − 1 ) + s t a i r s ( n − 2 )
我们可以得出,这就是斐波那契数列。
# 最后期望与你一起遇见更好的自己
扫码或搜索:方家小白
发送 290992
即可立即永久 解锁本站全部文章

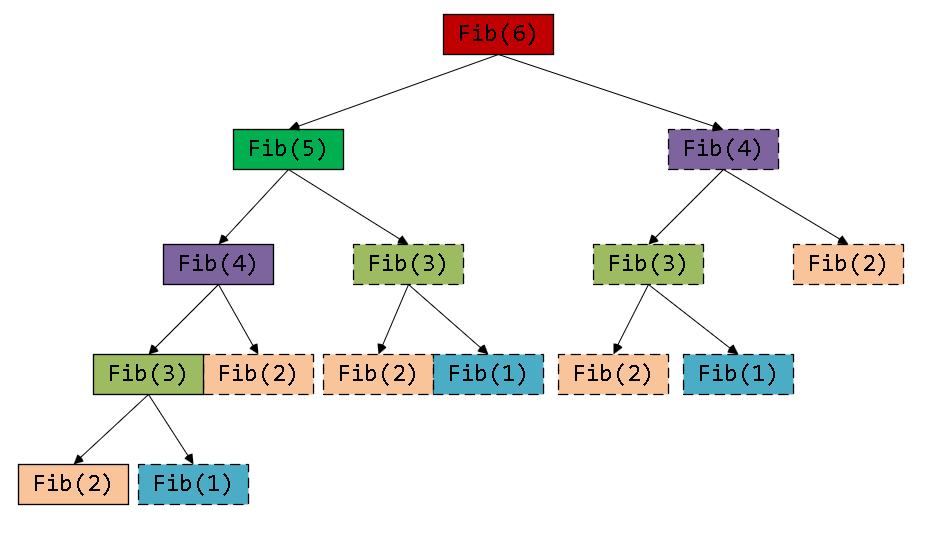 其中虚线边框的就不用再计算了。
其中虚线边框的就不用再计算了。